고마우미

문제

Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
class Node { public int val; public List<Node> neighbors; }
 
Test case format:
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
 
Example 1:

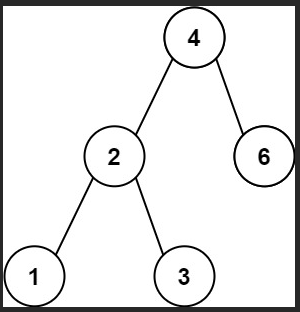
Input: adjList = [[2,4],[1,3],[2,4],[1,3]] Output: [[2,4],[1,3],[2,4],[1,3]] Explanation: There are 4 nodes in the graph. 1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3). 3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:

Input: adjList = [[]] Output: [[]] Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = [] Output: [] Explanation: This an empty graph, it does not have any nodes.
 
Constraints:
The number of nodes in the graph is in the range [0, 100].
1 <= Node.val <= 100
Node.val is unique for each node.
There are no repeated edges and no self-loops in the graph.
The Graph is connected and all nodes can be visited starting from the given node.

문제 접근

1. 탐색한 노드를 저장할 변수 저장

2. BFS 탐색을 위해 Queue에 첫번째노드의 값을 복사하여 새로운 Node를 생성해준 후 큐에 넣는다.

3. 전체노드를 탐색하며 탐색하지 않은 노드에 대해서 노드를 생성하며 간선을 연결한다.

풀이

import java.util.*;

class Solution {
  public Node cloneGraph(Node node) {
    if(node == null) return null;
   
    Node visited[] = new Node[101];
      
    Node firstNode = new Node(node.val);

    Queue<Node> q = new LinkedList<>();
    q.add(node);

    visited[firstNode.val] = firstNode;
    Node tempNode = null;
  
    while(!q.isEmpty()){
      tempNode = q.poll();
           
      for(Node n : tempNode.neighbors){
        if(visited[n.val] == null){
          visited[n.val] = new Node(n.val);
          q.add(n);
        }

        visited[tempNode.val].neighbors.add(visited[n.val]);
               
      }
    }
    return firstNode;
  }
}

문제

You are given two integer arrays nums1 and nums2 sorted in non-decreasing order and an integer k.
Define a pair (u, v) which consists of one element from the first array and one element from the second array.
Return the k pairs (u1, v1), (u2, v2), ..., (uk, vk) with the smallest sums.
 
Example 1:
Input: nums1 = [1,7,11], nums2 = [2,4,6], k = 3 Output: [[1,2],[1,4],[1,6]] Explanation: The first 3 pairs are returned from the sequence: [1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
Example 2:
Input: nums1 = [1,1,2], nums2 = [1,2,3], k = 2 Output: [[1,1],[1,1]] Explanation: The first 2 pairs are returned from the sequence: [1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]
Example 3:
Input: nums1 = [1,2], nums2 = [3], k = 3 Output: [[1,3],[2,3]] Explanation: All possible pairs are returned from the sequence: [1,3],[2,3]
 
Constraints:
1 <= nums1.length, nums2.length <= 10^5
-10^9 <= nums1[i], nums2[i] <= 10^9
nums1 and nums2 both are sorted in non-decreasing order.
1 <= k <= 10^4

문제접근

1. priorityQueue의 우선순위를 리스트의 합으로 선언한다.

2. pq에 모든 배열쌍을 추가한다.

3. pq에서 k번째까지 요소를 list에 add 한다.

---> 메모리 초과

import java.util.*;
import java.lang.Math;

class Solution {
    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        
        PriorityQueue<List<Integer>> pq = new PriorityQueue<>((a,b)-> (a.get(0) + a.get(1) -b.get(0) - b.get(1)));

        List<Integer> tempList;

        for(int i = 0; i < Math.min(nums1.length, k); i++){
            
            for(int j = 0; j < Math.min(nums2.length, k); j++){
                tempList = new LinkedList<Integer>();
                tempList.add(nums1[i]);
                tempList.add(nums2[j]);
                pq.add(tempList);
            }
        }

        List<List<Integer>> list = new LinkedList<>();

        for(int i = 0; i < k; i++){
            if(pq.isEmpty()) break;
            list.add(pq.poll());
        }


        return list;
    }
}

다른풀이 및 회고

import java.util.*;

public class Solution {

    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (b[0] + b[1])-(a[0]+a[1]));
        
        for (int i = 0; i < Math.min(nums1.length, k); i++) {
            for (int j = 0; j < Math.min(nums2.length, k); j++) {
                int[] cur={nums1[i], nums2[j]};
                if (pq.size() == k) {
                    int[] pk=pq.peek();
                    if(pk[0]+pk[1]>cur[0]+cur[1]){
                        pq.poll();
                        pq.offer(cur);
                    }
                    else break;
                }
                else pq.offer(cur);
            }
        }

        List<List<Integer>> result = new ArrayList<>();
        while (!pq.isEmpty()) {
            int[] pair = pq.poll();
            result.add(Arrays.asList(pair[0], pair[1]));
        }

        return result;
    }
}

접근 방식은 크게 다른게 없으나 peek을 통해 이전에 큰값을 poll 처리하고 새로운 값을 offer하면서 공간의 효율을 활용한것 같다. 

문제

Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.
 
Example 1:

Input: root = [4,2,6,1,3] Output: 1
Example 2:

Input: root = [1,0,48,null,null,12,49] Output: 1
 
Constraints:
The number of nodes in the tree is in the range [2, 10^4].
0 <= Node.val <= 10^5

문제접근

1. 트리를 순회하며 해당 트리의 값을 리스트에 추가한다.

2. 리스트를 정렬한다.

3. 리스트를 순회하며 최소값을 찾는다.

문제풀이

import java.lang.Math.*;

class Solution {

    static int min;
    public int getMinimumDifference(TreeNode root) {

        min = Integer.MAX_VALUE;
        
        List<Integer> list = new LinkedList<>();

        list.add(root.val);
        dfs(root, list);

        Collections.sort(list);

        int min = Integer.MAX_VALUE;


        for(int i = 1 ; i < list.size(); i++){
            min = Math.min(min,list.get(i) - list.get(i-1));
        }

        return min; 
    }

    public void search(TreeNode node, List list){
        if(node.left != null ){
            list.add(node.left.val);
            search(node.left, list); 
        }
        if(node.right != null){
            list.add(node.right.val);
            search(node.right, list); 
        }
    }
}

다른풀이 및 회고

class Solution {
       Integer res = Integer.MAX_VALUE, pre = null;
    public int getMinimumDifference(TreeNode root) {
        if (root.left != null) getMinimumDifference(root.left);
        if (pre != null) res = Math.min(res, root.val - pre);
        pre = root.val;
        if (root.right != null) getMinimumDifference(root.right);
        return res;
    }
}

처음에 내가 고려헀던 방향하고 유사한 느낌이다.

리스트에 추가할 필요없이 트리를 순회하면서 계산하여 최솟값을 계산하면되는데 root를 제외하고 연산하며 테스트 케이스에서 실패가 나와서 내가 인지하지 못하는 케이스가 있다 생각하여 리스트를 만들어 추가하였었다.

문제

A peak element is an element that is strictly greater than its neighbors.
Given a 0-indexed integer array nums, find a peak element, and return its index. If the array contains multiple peaks, return the index to any of the peaks.
You may imagine that nums[-1] = nums[n] = -∞. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in O(log n) time.
 
Example 1:
Input: nums = [1,2,3,1] Output: 2 Explanation: 3 is a peak element and your function should return the index number 2.
Example 2:
Input: nums = [1,2,1,3,5,6,4] Output: 5 Explanation: Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
 
Constraints:
1 <= nums.length <= 1000
-2^31 <= nums[i] <= 2^31 - 1
nums[i] != nums[i + 1] for all valid i.

문제접근

O(log n) 의 시간 복잡도를 가질려면 완전 탐색이 아닌 다른 접근법을 생각한다.

1. peak는 양 옆 보다 큰 수를 찾으면된다. (가장 큰수를 찾으면 해결)

2. 이분탐색을 통해 가장 큰 수를 반환한다.

문제 풀이

class Solution {
    public int findPeakElement(int[] nums) {
        int start = 0;
        int end = nums.length - 1;

        while (end > start) { 
            int mid = (start + end) / 2;
            if (nums[mid] < nums[mid + 1]) 
                start = mid + 1;
             else
                 end = mid;

        }
        return end;
    }
}